Trump overvalued
Note: I have revised the reasoning and conclusions of this post in a more recent post. Please see that post for my most recent thinking about this market. Also, Trump did in fact win majorities in all five states. I did a postmortem of this bet here.
I spotted an irrationality on the prediction markets today that caused me to update negatively against the institution's usefulness as an information aggregator. I've previously encountered (and written about) prediction market irrationalities; this is another one for the books.
A new market recently surfaced, on whether Trump will exceed 50% in all five April 26 primaries. The market struck me as abnormally high at 20%:
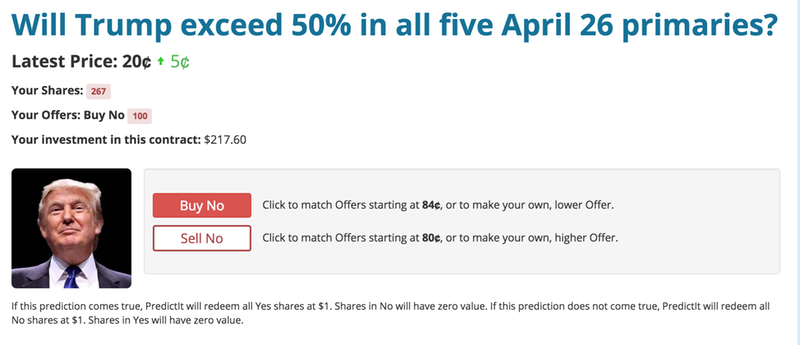
This market is asking about the conjunct of five events – Trump winning more than 50% of the primary vote in each of the states voting on April 26.
The conjunct probability of five events is the product of the probabilities of each event (assuming independence):
p(Trump wins 50% in 5 states) =
p(Trump wins 50% in Connecticut) * p(Trump wins 50% in Delaware) *
p(Trump wins 50% in Maryland) * p(Trump wins 50% in Pennsylvania) *
p(Trump wins 50% in Rhode Island)
It's safe to assume independence in this case because the five primaries (Connecticut, Delaware, Maryland, Pennsylvania, Rhode Island) will all occur at roughly the same time, in the same time zone. It would be unlikely for the result of one of these primaries to influence the result of another, so we will assume that there's no inter-primary influence.
Let's step back from the "wins 50%" part of this for a moment, and just look at the probability that Trump wins in each state. Independence still holds, so this is given by:
p(Trump wins all 5 states) =
p(Trump wins Connecticut) * p(Trump wins Delaware) *
p(Trump wins Maryland) * p(Trump wins Pennsylvania) *
p(Trump wins Rhode Island)
538 is my go-to for primary forecasting. For each primary, 538 provides two forecasts, 'polls-only' (which just aggregates state-level polling data) and 'polls-plus' (which aggregates state-level polling along with national polling and endorsements). It's unclear which method is more accurate, though I tend to take polls-plus more seriously.
Trump polls well, so the polls-plus method is more conservative. Plugging 538 polls-plus numbers into the above equation give us:
p(Trump wins all 5 states) =
0.90 * 0.99 * 0.81 * 0.86 * 0.99 = 0.61
Note: 538 hasn't modeled the Delaware and Rhode Island primaries because there hasn't been much polling in those states. To be generous to Trump, I assumed a 99% chance of victory for those primaries.
The conjunct probability of winning all five states is 61%, using polls-only forecasts. So, under these assumptions, Trump has a 61% chance of sweeping on the 26th (using polls-only, it's substantially higher: 85%).
It looks like Trump has a very good chance of winning all five states on April 26th. Let's return to the question of whether he will win majorities in those states.
So far, Trump has only won >50% of the vote in one state (New York), and usually wins 30% to 40% of the vote. To think that he would win >50% in the April 26th primaries, you would have to think that they were as favorable to Trump as New York, where he had home state advantage.
Taking a look at recent polling, Trump's current polling averages are in the low- to mid-40s in Connecticut, Maryland, and Pennsylvania. To think that he would win by >50% in these states, you'd have to think that he will outperform his polls in each state (historically, Trump has underperformed his polling).
The main consideration in this market is what to think of the relationship between winning a state and winning a majority in that state. If we think Trump has a reasonable chance of taking 50% of the vote in states he wins (e.g. if we think that April 26th states will be similar to New York, where Trump dominated), then this market is likely undervalued. Here's an example of that scenario, where we assume that for each state, the probability of Trump taking 50% of the vote is 10 points less than the probability of Trump winning the state (this scenario uses polls-plus 538 forecasts, which, as mentioned above, I prefer to polls-only):
p(Trump wins 50% in 5 states) =
0.80 * 0.89 * 0.71 * 0.76 * 0.89 = 0.34
34%. So following this view, the market is actually quite undervalued, by nearly 2x!
Now let's consider an alternate scenario, where we believe that Trump is highly unlikely to take the majority of votes in states he wins (e.g. we believe that New York was an exceptional performance due to his home state advantage, and other states will have margins closer to his previous victories). To get a read on how likely we should consider majority victories, we can estimate Trump's majority victory base rate: to date, 35 states have held primaries or caucuses (not including D.C. or territories), and Trump has won a majority in one of them. 1/35 = ~3%. This is likely an underestimate, because as presidential candidates drop out, Trump's share of the vote will increase, so let's say that for each state going forward, there's a 6% chance of Trump winning a majority. Further, Rhode Island and Connecticut are very close to New York, so let's give them a 'close to home' bonus and bump them up to 30% each. This scenario implies:
p(Trump wins 50% in 5 states) =
0.30 * 0.30 * 0.06 * 0.06 * 0.06 = 0.000019
0.000019 is just a sliver of a percent. Because I'm bad at thinking about probabilities that are that small, let's call this <1%. So, following this view, there's a <1% chance that Trump wins a majority of the vote in all five April 26th primaries.
Depending on how we approach the problem, we arrive at very different estimates of how likely Trump is to win majorities in the five April 26th primaries (<1% compared to 34%). At 20%, the PredictIt market is splitting the difference. If we thought both of these views were equally valid, 20% would be a reasonable place for the market to be.
However, I think the second method is more grounded than the first. By using a base rate, it takes into account Trump's track record of achieving majority wins. It also aligns better than recent polling, which suggests that Trump will take 40-46% of the vote in the three states where polls are available, as well as aligning with the historical expectation that Trump will match or underperform his polling, rather than exceeding it. Also, under the first method (estimating the chance of majority victory by adjusting the chance of victory down by an arbitrary amount), it's not clear what adjustment would be appropriate, and a reasonable-seeming adjustment (down by 10 points) yields very sunny results.
Personally, I'm applying very little weight to the first method, so my guess is that the real probability of Trump sweeping majorities on April 26th is closer to 1% than 20%. I bought some 'No' shares, obviously.
My guess is that some participants in the PredictIt market are betting based on a form of method 1 reasoning, and others are making impulsive bets without thinking through the probabilities these bets imply. Something similar is likely happening in other Trump-centric markets as well (Will there be a GOP brokered convention? has been in a slow slide for a couple weeks now, and after New York, Trump's chances of being the Republican nominee have more than rebounded). Unfortunately, assessing just how overvalued these markets are is more difficult than the current case. I'm anti-Trump in both, though it's possible that the Trump hysteria persists until the convention, in which case there would be no market correction, and the overvalued shares would resolve to $1.
[rereads: 6, edits: typo corrections, phrasing tweaks, making the code blocks look pretty, added a pointer to the 'revised' post and the postmortem. Also, when writing a previous version of this post, I had mistakenly flipped a probability I was considering, then spent several paragraphs and a couple of hours building a case for the situation that the flipped probability implied. I realized this a few minutes after publishing the post (and sending it to some friends), felt very silly, then reworked my argument based on the correct probabilities. This was a good lesson in the dangers of motivated reasoning – taking an incorrect probability as true, I built a case around it that seemed convincing and obviously correct, and when writing it never occurred to me that I might be honing in on an absurd conclusion.]